- 判断PCA中需要多少主成分
a、根据先验经验和理论知识判断主成分数
b、根据要解释变量方差的积累值的阈值来判断需要的主成分数,如选择使累积方差达到80%的主成分个数
c、通过检查变量间 k*k 的相关系数矩阵来判断保留的主成分数(根据相关系数矩阵的特征值,选择特征值大于1的主成分)
1、最常见的是基于特征值的方法
每个主成分都与相关系数矩阵的特征值相关联,第一主成分与最大的特征值相关联,第二主成分与第二大的特征值相关联,依此类推。Kaiser-Harris准则建议保留特征值大于1的主成分,特征值小于1的成分所解释的方差比包含在单个变量中的方差更少
2、Cattell碎石检验
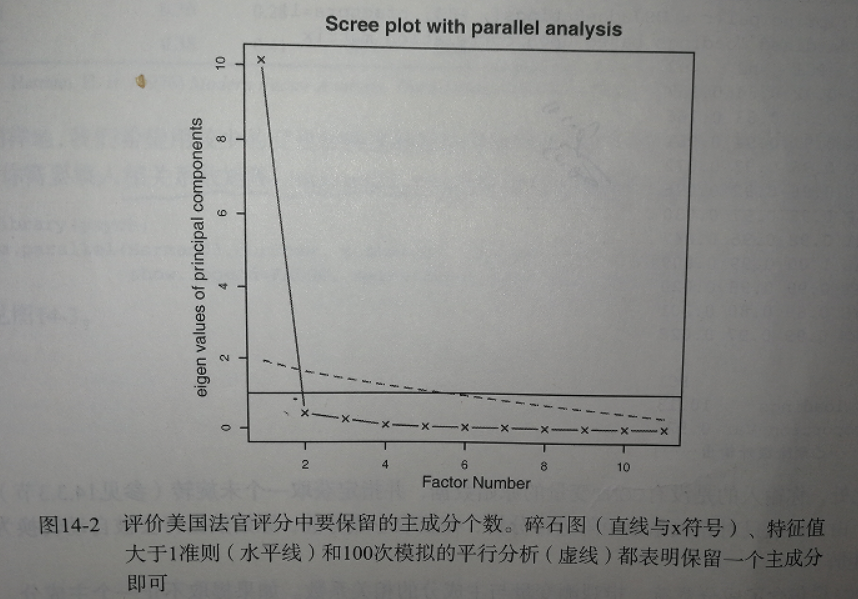
Cattell碎石检验则绘制了特征值与主成分数的图形。这类图形可以清晰的展示图形弯曲状况,在图形变化最大处之上的主成分都可以保留。
3、平行分析
还可以进行模拟,依据初始矩阵相同大小的随机数据矩阵来判断要提取的特征值,若基于真实数据的某个特征值大于一组随机数据矩阵相应的平均特征值,那么该主成分可以保留
- 对特征值判别准则进行评价
fa.parallel()函数 同时对上述1~3的准则进行评价,对于11中评分(删去了CONT变量),代码如下
#同时对三种特征判别准则进行评价> library(psych)> fa.parallel(USJudgeRatings[,-1],fa="pc",n.iter = 100, #n.iter 100个随机数+ show.legend = FALSE,main = "Scree plot with parallel analysis")#绘制的图形如下The estimated weights for the factor scores are probably incorrect. Try a different factor extraction method.Parallel analysis suggests that the number of factors = NA and the number of components = 1 #建议nfactors=1
on method. P
x
1
#同时对三种特征判别准则进行评价
2
> library(psych)
3
> fa.parallel(USJudgeRatings[,-1],fa="pc",n.iter = 100, #n.iter 100个随机数
4
+ show.legend = FALSE,main = "Scree plot with parallel analysis")#绘制的图形如下
5
The estimated weights for the factor scores are probably incorrect. Try a different factor extraction method.
6
Parallel analysis suggests that the number of factors = NA and the number of components = 1 #建议nfactors=1